
iPhone sales are plunging. Here's why.

Nikki Haley lands new gig after dropping out of GOP primary

What we know about Channing Tatum and Jenna Dewan's financial legal battle
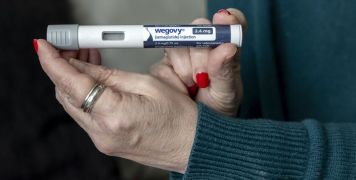
'Miracle' weight loss drugs have made health disparities worse, doctors say

'Go home': Over-tourism sparks angry backlash in Spain
Stories for you
- WorldUSA TODAY
California valedictorian will no longer give graduation speech over 'alarming' discussion
The University of Southern California says Asna Tabassum will no longer speak at the ceremony after the discussion about her selection took on "an alarming tenor."
4K3 min read - SportsYahoo Sports
WNBA Draft winners and losers: As you may have guessed, the Fever did pretty well. The Liberty? Perhaps not
Here are five franchises who stood out, for better or for worse.
7304 min read - BusinessReuters
Big banks led by Citi continue layoffs amid pressure to cut costs
U.S. banking giants continued to shed employees in the first quarter, with Citigroup seeing the biggest drop. Headcount at Citi declined by 2,000 employees after the third-largest U.S. lender completed a sweeping reorganization aimed at improving profits and reducing management layers. Bank of America, Wells Fargo and PNC Financial together cut more than 2,000 jobs in the three months ended March 31 compared with the previous quarter.
12 min read - SportsUSA TODAY Sports
Caitlin Clark is best thing to happen to WNBA. Why are some players so frosty toward her?
Caitlin Clark playing in the WNBA could lift women's sports to incredible heights, which makes any resentment toward her just baffling.
1.9K8 min read - SportsCNN
Chinese runner’s win invites suspicion after rivals appear to step aside
Chinese runner He Jie’s victory in Sunday in the Beijing Half Marathon is facing a probe after his win was called into question by Chinese internet users because a trio of African runners appeared to deliberately slow down to let him win.
8763 min read - BusinessBuzzFeed
Non-Americans Are Convinced Only A Handful Of Americans Can Comprehend These 32 Things
I truly can't comprehend a world where RadioShack still exists, but apparently, it does!
14 min read - SportsDetroit Free Press
Michigan football handed three-year probation, recruiting penalties and fine by NCAA
The Michigan football program has been placed under a three-year probation and will get recruiting penalties and a fine by the NCAA. Here's why:
21 min read - CelebrityBuzzFeed News
Katy Perry Was Forced To Hold A Cushion Over Her Chest And Hide Under The “American Idol” Judges' Desks After Suffering A Seriously Awkward Wardrobe Malfunction Live On Air
“You know it's serious fashion when the power tools come out.”View Entire Post ›
682 min read - LifestyleMashed
No, Drumsticks Aren't Actually Made With Real Ice Cream
The iconic Drumstick is ingrained in our collective memory as a favorite childhood treat. But did you know this ice cream cone isn't, well, ice cream?
44 min read - LifestyleBuzzFeed
I'm Pretty Much The Dumbest Guy On Earth So These 21 Absolutely Incredible Pictures Absolutely Put My Brain In A Blender Immediately After I Saw Them
I am flabbergasted.
963 min read - USBuzzFeed
"Imagine The Lawsuit If That Happened Today": Older Adults Revealed 29 Things That Used To Be "Normal" In Schools
"The older junior and senior-aged kids were allowed to drive the buses on the rural routes. One of our drivers, who was a senior, used to hit a big hill at top speed, and it would make the fire escape door fly off the back of the bus."
66 min read - LifestyleYahoo Life Shopping
Grab a viral anti-aging snail serum for $13 (nearly 50% off) — plus other incredible price cuts we found today
Shop massive spring savings on beloved brands, which include Dyson, Apple, Ninja and more.
01 min read - LifestyleApartment Therapy
Marshalls Is Selling the "Cutest" $30 Maximalist-Inspired Kitchen Find
These glasses are so pretty that you won’t use any of your other cups.
01 min read - NewsCNN
VideoBob Costas on what Johnnie Cochran told him privately after the OJ Simpson trial
CNN’s Bob Costas speaks with CNN’s Jake Tapper
650 - CelebrityE! News
Proof Tom Schwartz & New Girlfriend Are Serious After This Milestone
Vanderpump Rules' Tom Schwartz shared rare insight into his new relationship with girlfriend Sophia Skoro on The Viall Files and revealed if he's ready to finally start a family.
07 min read - ScienceThe Weather Network
La Niña will make a comeback this summer as El Niño finally fades
The revised forecasts issued by scientists have been revealed, and the verdict is clear: La Niña will make a comeback
311 min read - LifestyleINSIDER
I worked at Disney World for over 3 years. Here are answers to 8 questions guests are too embarrassed to ask.
As a former Disney World cast member who spent three years working in the parks, I've answered plenty of "embarrassing" questions from tourists.
1096 min read - USHuffPost
'Gross And Vulgar' Rob Schneider Comedy Set Reportedly Cut Short At GOP Event
The "SNL" alum lashed out following the report, telling TMZ it was "woke bulls**t."
3231 min read - LifestyleBuzzFeed
People Are Sharing What They Think Screams "I'm A Bad Parent"
From giving kids no structure to using them as a pawn against the other parent, these are just some of the behaviors people feel should be avoided at all costs.
26 min read - LifestyleNY Post
I’m an ex-Mormon — here’s why members of my former church look alike
Alyssa Grenfell pointed out that Ryan Gosling, 43, was born Mormon, noting in her video caption that "he has Mormon face."
1K3 min read



















